Beschreibung
This Application Note explains how to convert the raw output from an electrolytic tilt sensor into degrees.
Linearer Bereich und Arbeitsbereich von Neigungssensoren
Der Messbereich eines elektrolytischen Neigungssensors kann auf zwei Arten beschrieben werden: linearer Bereich und Betriebsbereich. Der Arbeitsbereich ist der Bereich, in dem der Sensor einen monotonen Ausgang liefert, aber ansonsten keine definierten Eigenschaften aufweist (er ist nicht linear). Der lineare Bereich ist der Teil des Arbeitsbereichs, in dem der Ausgang innerhalb eines bestimmten Prozentsatzes linear ist. Abbildung 1 zeigt den Unterschied zwischen den beiden Bereichen.
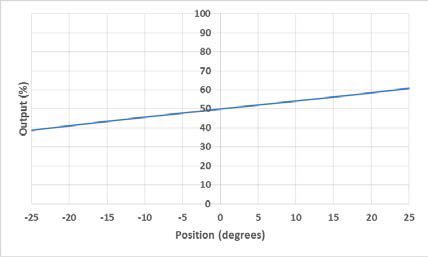
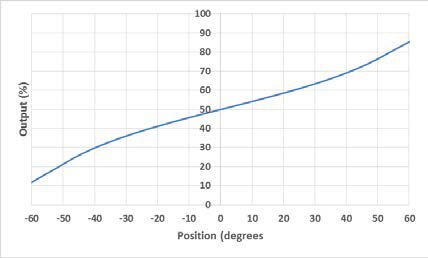
Abbildung 1 Linearer Bereich (links) und Betriebsbereich (rechts).
Lineare Approximation
Um den Neigungswinkel innerhalb des linearen Bereichs zu finden, ist es notwendig, eine lineare Funktion zu finden, die mit dem Ausgang des Sensors übereinstimmt. Dies wird die Funktion der Linie im linken Diagramm in Abbildung 1 sein. Diese Funktion ist unten angegeben:
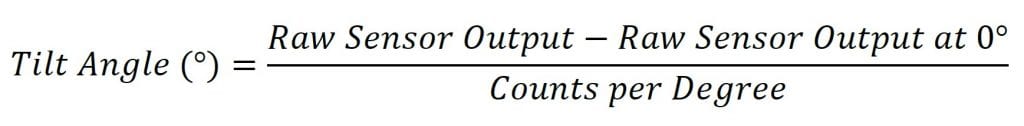
Der rohe Sensorausgang in dieser Formel ist der Ausgang des Sensors. Dies ist normalerweise in Zählungen, aber andere Einheiten können verwendet werden, je nachdem, wie die Sensorausgabe gelesen wird.
Für die beiden anderen Werte müssen Proben des Sensors in bestimmten Winkeln genommen werden. Diese Winkel können mithilfe eines anderen Sensors, eines digitalen Winkelmessers oder einer anderen Methode zur Bestimmung von Winkeln ermittelt werden. Der Rohsensorausgang bei 0° ist nur der Ausgang, wenn der Sensor waagerecht ist.
Die Zählungen pro Grad (das ist die Steigung der Linie) wird mit der folgenden Formel berechnet:
![]()
Der lineare Bereich wird aus dem Datenblatt des Sensors entnommen. Die Rohausgänge sind der Sensorausgang an den Rändern des linearen Bereichs. Zum Beispiel würden bei einem Sensor mit einem linearen Bereich von ±25° die Rohausgänge bei +25° und -25° abgetastet werden. Beachten Sie, dass diese Abtastwerte nur einmal zur Erstellung der Funktion genommen werden müssen; die Konvertierung der Neigung kann dann mit den abgetasteten Werten durchgeführt werden.
Nehmen wir an, wir haben einen Sensor 0717-4319-99 mit einem 16-Bit-Ausgang (0 bis 65535), den wir in Grad umrechnen möchten. Dies ist ein Zweiachsensensor mit einem linearen Bereich von ±20°. Da es sich um einen Zweiachsensensor handelt, benötigen wir 2 Formeln: eine für die X-Achse und eine für die Y-Achse. Als erstes werden wir die Formel für die X-Achse finden. Wir beginnen mit Stichproben bei 0° und ±20° und finden die folgenden Messwerte.
Neigung der X-Achse bei -20° = 26055
X-Achse Neigung bei 0° = 33234
X-Achse Neigung bei ±20° = 40379
Jetzt können wir diese Proben verwenden, um die Zählungen pro Grad zu berechnen:
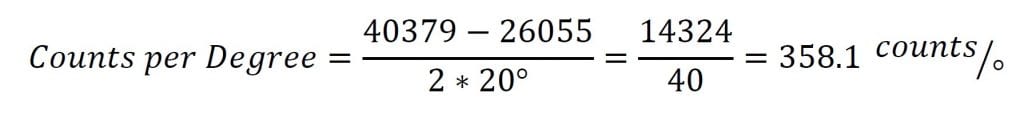
Die Zählungen pro Grad und Nullprobe können dann in die Formel eingesetzt werden, um die unten stehende Umrechnung zu erhalten:

Wenn eine Messung der Y-Achse erforderlich ist, führen Sie diese Schritte erneut mit Proben der Y-Achse durch.
Wenn wir nun eine Messung von diesem Sensor haben, die wir in Grad umrechnen möchten, können wir diese neue Formel verwenden. Wenn wir zum Beispiel einen X-Ausgang von 29655 haben, können wir die Formel verwenden, um den Neigungswinkel zu bestimmen:
![]()
Ungefähre Zählungen pro Grad
Aufgrund von leichten Abweichungen, die durch den Herstellungsprozess verursacht werden, sollte die Umrechnungsfunktion für jeden spezifischen Sensor berechnet werden. Dies ist jedoch nicht immer machbar. Die folgende Tabelle enthält durchschnittliche Zählwerte pro Grad und 0°-Werte, die für die Berechnungen verwendet werden können. Beachten Sie, dass die Verwendung dieser Werte zu weniger genauen Messungen führt als die Erstellung einer Funktion für den spezifischen Sensor. Alle Werte beziehen sich auf einen 16-Bit-Ausgang (0-65535). Für Sensoren, die nicht in der Tabelle aufgeführt sind, muss der Benutzer das oben beschriebene Verfahren befolgen, um eine Umrechnung zu finden.
| Sensor | Zählungen pro Grad | Null-Grad |
| 0703-1602-99, 0729-1765-99 | 976 | 32768 |
| 0703-0711-99 | 17582 | 32768 |
| 0717-4303-99 | 736 | 32768 |
| 0717-4304-99 | 268 | 32768 |
| 0717-4305-99 | 188 | 32768 |
| 0717-4306-99 | 188 | 32768 |
| 0717-4311-99 | 268 | 32768 |
| 0717-4313-99 | 342 | 32768 |
| 0717-4314-99 | 335 | 32768 |
| 0717-4316-99 | 756 | 32768 |
| 0717-4317-99 | 569 | 32768 |
| 0717-4318-99, 0729-1751-99, 0729-1752-99, 0729-1753-99, 0729-1754-99, 0729-1755-99, 0729-1759-99, 0729-1760-99 |
284 | 32768 |
| 0717-4319-99 | 363 | 32768 |
| 0717-4321-99 | 758 | 32768 |
| 0717-4322-99 | 594 | 32768 |
| 0737-0101-99 | 2887 | 32768 |
| 0737-1203-99 | 12765 | 32768 |
Mehrpunkt-Interpolation
Die Mehrpunkt-Interpolationsmethode verwendet im Voraus entnommene Proben, um die Messung in Grad abzuleiten. Die Genauigkeit dieser Methode hängt von der Anzahl und der Verteilung der Stichproben ab; jedoch liefert selbst die Entnahme von 3 Stichproben im Allgemeinen ein besseres Ergebnis als eine lineare Näherung.
Die Stichprobenverteilung ist einer der wichtigsten Faktoren, um eine genaue Umrechnung zu erreichen. Umrechnungen, die nahe an Proben liegen, sind genauer. Aus diesem Grund führen Proben, die näher beieinander liegen, zu genaueren Umrechnungen. Diese Proben sollten über den gesamten Bereich des Sensors genommen werden. Je nach Anwendung können sie gleichmäßig über den gesamten Bereich verteilt sein oder in einem Bereich konzentriert werden, in dem Präzision erforderlich ist.
Um einen Rohwert in Grad umzurechnen, identifizieren Sie zwei Referenzproben. Dies sind die beiden Proben, die der Messung in jeder Richtung am nächsten sind. Finden Sie dann eine lineare Annäherung zwischen den beiden Abtastungen und bilden Sie die Rohausgabe auf diese Annäherung ab. Der Punkt auf dieser Linie gibt die Neigung des Sensors in Grad an. Die Grafik in Abbildung 2 zeigt eine Visualisierung dieses Konzepts.
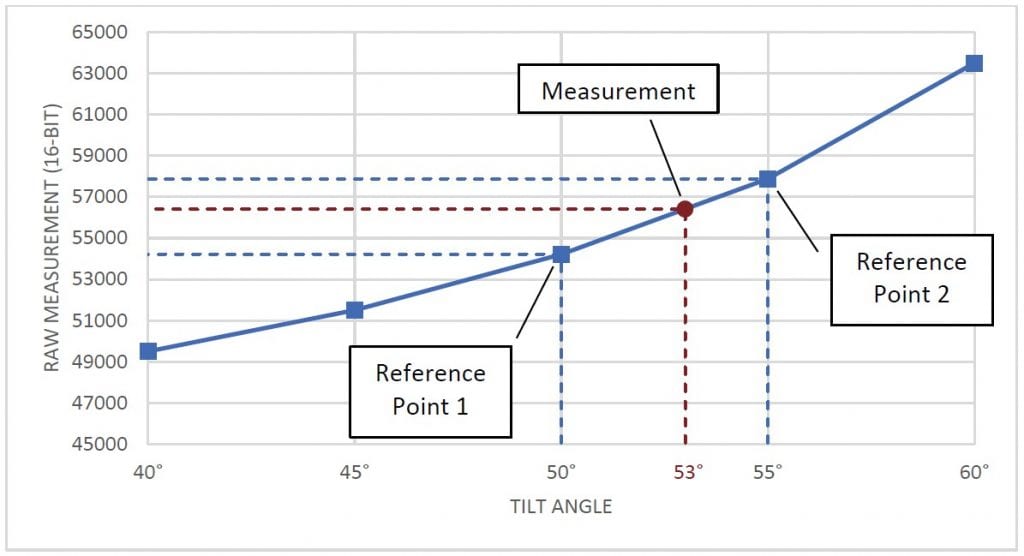
Abbildung 2 Diagramm, das Proben, Referenzproben und die Messung anzeigt.
Die Formel für diese Umrechnung ist unten dargestellt.

Nehmen wir an, wir haben eine Rohmessung von 56412 von einem Neigungssensor mit einem Arbeitsbereich von ±60°. Nehmen wir außerdem an, dass wir bereits Stichproben in 5°-Intervallen genommen haben, um sie für die Umrechnung zu verwenden. Durch den Vergleich von 56412 mit den Abtastwerten bestimmen wir, dass unsere beiden Referenzpunkte bei 50° (54213) und 55° (57878) liegen werden. Wir können dann die Formel verwenden, um den Winkel zu berechnen:
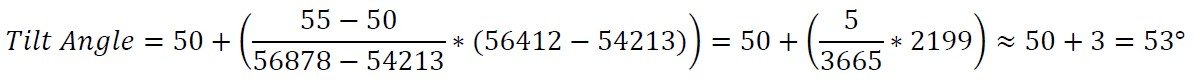
Daher ist unsere endgültige Messung 53°.
Diese Methode kann verwendet werden, um Messungen aus einem beliebigen Bereich innerhalb des Arbeitsbereichs des Sensors in Grad umzurechnen. Sie erreicht auch eine bessere Genauigkeit als die lineare Näherung. Sie erfordert jedoch eine große Anzahl von genauen Abtastungen, um die besten Ergebnisse zu erzielen.
Polynomiale Interpolation
Die polynomiale Interpolation kann verwendet werden, um genaue Messungen zu erzielen, ohne viele Proben zu nehmen. Diese Methode verwendet Proben, um eine Polynomgleichung zu finden, die eine genaue Umwandlung über den Betriebsbereich des Sensors liefert.
Die entnommenen Stichproben werden verwendet, um eine Polynomgleichung zu entwickeln, die den Sensorausgang beschreibt. Sie benötigen mindestens N-1 Abtastungen, um ein Polynom vom Grad N abzuleiten. Zum Beispiel erzeugen 7 Abtastungen ein Polynom vom Grad 6. Sie können auch mehr Abtastwerte verwenden, um ein Polynom niedrigeren Grades zu erstellen, aber dies hat im Allgemeinen eine geringere Genauigkeit als die Erstellung eines Polynoms höheren Grades mit denselben Punkten.
Es kann eine beliebige Anzahl von Stichproben verwendet werden, wir empfehlen jedoch, mindestens 3 Stichproben zu nehmen. Die Verwendung von 2 Stichproben würde funktionieren, führt aber zu einer linearen Annäherung. Beachten Sie, dass die Genauigkeit bei Polynomen vom Grad 7 oder höher kaum verbessert wird.
Während das Polynom manuell bestimmt werden kann, ist es viel einfacher, es mit Hilfe von Software zu berechnen. Eine einfache Methode ist die Verwendung der Anpassungsgeraden von Microsoft Excel; diese ist jedoch möglicherweise nicht genau genug für eine brauchbare Umrechnung. Wolfram Alpha ist eine genauere Option, aber die Gleichung muss immer noch manuell gelöst werden. Die beste Option ist die Verwendung einer Programmierbibliothek. Zum Beispiel kann die Methode Polynomial.fit() aus der Python-Bibliothek NumPy verwendet werden. Der folgende Code zeigt, wie damit ein Polynom 6. Ordnung aus 7 Punkten erzeugt werden kann:
import numpy.polynomial.polynomial koeffizienten = numpy.polynomial.polynomial.Polynomial.fit( [56668, 46553, 36140, 32845, 31207, 21913, 9586], # Rohwerte [60, 42, 12, 0, -6, -36, -60], # entsprechende Winkelwerte zu den Rohwerten 6) # Ordnung des Polynoms print(koeffizienten) # Ausgabe: # [-7.88427627e+01 2.57631617e-03 -7.71958174e-08 -1.75354175e-13 # 2.17551410e-16 -5.89635260e-21 4.45379575e-26]
Beachten Sie, dass es bei der Verwendung einer Funktion wie dieser wichtig ist, die Ordnung richtig anzugeben. Zum Beispiel erzeugen 4 Proben ein Polynom 3. Wenn jedoch 4 als Ordnung angegeben wird, wird die Bibliothek eine zufällige Vermutung anstellen, um eine Gleichung zu erstellen. Dies führt zu weniger genauen Umrechnungen.
Das von Polynomial.fit() zurückgegebene Array sind die Koeffizienten des Polynoms. Basierend auf der obigen Ausgabe würde die Gleichung lauten:
Winkel = (4,45e-26)x6- (5,89e-21)x5+ (2,17e-16)x4- (1,75e-13)x3- (7,72e-8)x2+ (2,57e-3)x1- 78,84
Diese Funktion kann dann verwendet werden, um unbekannte Winkel zu lösen, indem der Rohwert für x eingesteckt wird. Angenommen, wir haben die obige Funktion und einen Rohwert von 41643. Wir können den Winkel mit den folgenden Berechnungen finden:
Winkel = (4,45e-26)(41643)6 - (5,89e-21)(41643)5 + (2,17e-16)(41643)4 - (1,75e-13)(41643)3 - (7,72e-8)(41643)2 + (2,57e-3)(41643)1 - 78,84
Winkel = 232,264 - 738,402 + 654,227 - 12,663 - 133,868 + 107,285 - 78,842 = 30,002°
Wenn Sie die oben gezeigte NumPy-Bibliothek verwenden, können Sie dies mit der Methode polyval() tun.
print(numpy.polynomial.polynomial.polyval(41643, coefficients.convert(.coef)) # Output: 30.001695321007
Beachten Sie, dass das Ergebnis dieser Berechnung sehr empfindlich auf jede Änderung der Eingabe reagiert. Wenn zum Beispiel die obigen Koeffizienten auf 3 signifikante Stellen gerundet werden (wie geschrieben), ist das Ergebnis der Gleichung 31°. Aus diesem Grund ist es wichtig, bei der Winkelberechnung mit dieser Methode keine Werte zu runden.





