Descripción
Esta nota de aplicación explica cómo convertir la salida bruta de un sensor de inclinación electrolítico en grados.
Rango lineal y rango de operación de los sensores de inclinación
An electrolytic tilt sensor’s measurement range can be described in two ways: linear range and operating range. The operating range is the range over which the sensor will give a monotonic output but otherwise has no defined characteristics (it is non-linear). The linear range is the portion of the operating range where the output is linear to within a certain percentage. Figure 1 shows the difference between the two ranges.
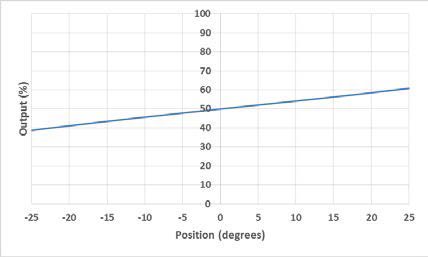
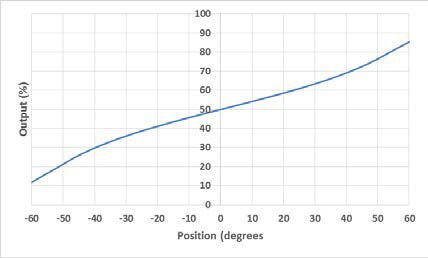
Figura 1 Rango lineal (izquierda) y rango de operación (derecha).
Aproximación lineal
To find the tilt angle within the linear range, it is necessary to find a linear function that matches the output of the sensor. This will be the function of the line in the left graph in Figure 1. This function is given below:
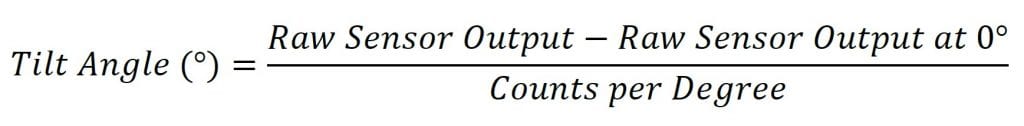
La salida bruta del sensor en esta fórmula es la salida del sensor. Esto suele ser en recuentos, pero pueden usarse otras unidades dependiendo de cómo se lea la salida del sensor.
Los otros dos valores requerirán tomar muestras del sensor en ciertos ángulos. Estos ángulos pueden ser determinados usando otro sensor, un transportador digital, o cualquier otro método para determinar los ángulos. La salida bruta del sensor a 0° es sólo la salida cuando el sensor está nivelado.
The counts per degree (which is the slope of the line) are calculated using the following formula:
![]()
The linear range is obtained from the datasheet for the sensor. The raw outputs will be the sensor output at the edges of the linear range. For example, for a sensor with a linear range of ±25°, the raw outputs would be sampled at +25° and -25°. Note that these samples will only need to be taken once to create the function; converting tilt can then be done using the sampled values.
Let’s say we have a 0717-4319-99 sensor with a 16-bit (0 to 65535) output we would like to convert to degrees. This is a dual axis sensor with a linear range of ±20°. Since it is a dual axis sensor, we will need 2 formulas: one for the X axis and one for the Y axis. First, we will find the X axis formula. We start be taking samples at 0° and ±20° and find the following measurements.
Inclinación del eje X a -20° = 26055
Inclinación del eje X a 0° = 33234
Inclinación del eje X a ±20° = 40379
Ahora podemos usar estas muestras para calcular los conteos por grado:
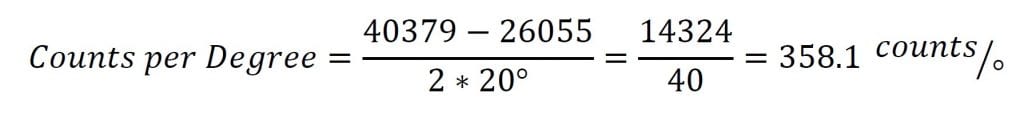
The counts per degree and zero samples can then be plugged into the formula to give the conversion below:

Si es necesaria una medición del eje Y, siga estos pasos de nuevo con muestras del eje Y.
Now, whenever we have a measurement from this sensor we would like to convert to degrees, we can use this new formula.
For example, if we have an X output of 29655, we can use the formula to determine the tilt angle:
![]()
Recuentos aproximados por grado
Debido a las ligeras variaciones causadas por el proceso de fabricación, la función de conversión debe ser calculada para cada sensor específico. Sin embargo, esto no siempre es factible. En la tabla siguiente se indican los recuentos medios por grado y los valores de 0° que pueden utilizarse en los cálculos. Tenga en cuenta que la utilización de estos valores dará lugar a mediciones menos precisas que la creación de una función para el sensor específico. Todos los valores son para una salida de 16 bits (0-65535). Los sensores que no están en la tabla requerirán que el usuario siga el procedimiento anterior para encontrar una conversión.
| Sensor | Recuentos por grado | Cero grados |
| ApexTwo™ | 284 | 32768 |
| F203-00A-212-00 | 17582 | 32768 |
| F225-00T-003-01 | 976 | 32768 |
| 0703-0711-99 | 17582 | 32768 |
| 0703-1602-99 | 976 | 32768 |
| 0703-1603-99 | 976 | 32768 |
| 0717-4303-99 | 736 | 32768 |
| 0717-4304-99 | 268 | 32768 |
| 0717-4305-99 | 188 | 32768 |
| 0717-4306-99 | 188 | 32768 |
| 0717-4311-99 | 268 | 32768 |
| 0717-4313-99 | 342 | 32768 |
| 0717-4314-99 | 335 | 32768 |
| 0717-4316-99 | 756 | 32768 |
| 0717-4317-99 | 569 | 32768 |
| 0717-4318-99 | 284 | 32768 |
| 0717-4319-99 | 363 | 32768 |
| 0717-4321-99 | 758 | 32768 |
| 0717-4322-99 | 594 | 32768 |
| 0729-1751-99 | 284 | 32768 |
| 0729-1752-99 | 284 | 32768 |
| 0729-1753-99 | 284 | 32768 |
| 0729-1754-99 | 284 | 32768 |
| 0729-1755-99 | 284 | 32768 |
| 0729-1759-99 | 284 | 32768 |
| 0729-1760-99 | 284 | 32768 |
| 0729-1765-99 | 976 | 32768 |
| 0729-1767-99 | 284 | 32768 |
| 0729-1768-99 | 284 | 32768 |
| 0729-1769-99 | 284 | 32768 |
| 0737-0101-99 | 2887 | 32768 |
| 0737-1203-99 | 41942-57670 | 32768 |
Interpolación multipunto
El método de interpolación multipunto utiliza muestras tomadas con antelación para derivar la medición en grados. La precisión de este método dependerá del número y la distribución de las muestras; sin embargo, incluso tomando 3 muestras generalmente se obtiene un mejor resultado que con una aproximación lineal.
Sample distribution is one of the most important factors in reaching an accurate conversion. Conversions close to samples will be more accurate. Because of this, samples taken closer together will result in more accurate conversions. These samples should be taken across the entire range of the sensor. Depending on the application, they can be evenly dispersed evenly across the entire range or focused in one region where precision is necessary.
To convert a raw value to degrees, identify two reference samples. These are the two samples that are closest to the measurement in each direction. Then, find a linear approximation between the two samples and map the raw output onto this approximation. The point on this line will give the sensor’s tilt in degrees. The graph in Figure 2 shows a visualization of this concept.
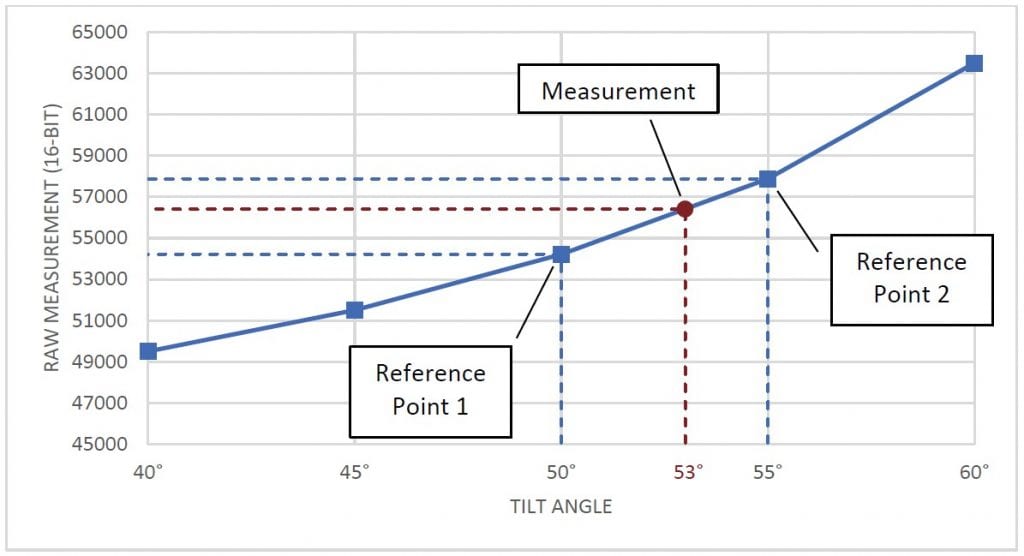
Figura 2 Gráfico que muestra las muestras, las muestras de referencia y la medición.
La fórmula de esta conversión se muestra a continuación.

Digamos que tenemos una medición en bruto de 56412 de un sensor de inclinación con un rango de operación de ±60°. Además, supongamos que ya tomamos muestras a intervalos de 5° para usarlas en la conversión. Comparando 56412 con las muestras, determinamos que nuestros dos puntos de referencia estarán a 50° (54213) y 55° (57878). Podemos entonces usar la fórmula para calcular el ángulo:
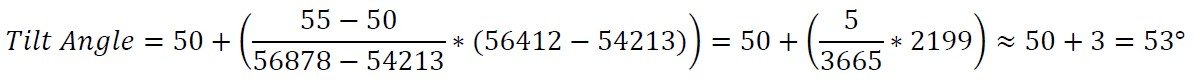
Por lo tanto, nuestra medición final es de 53°.
Este método puede utilizarse para convertir las mediciones de cualquier lugar dentro del rango de operación del sensor a grados. También logrará una mayor precisión que la aproximación lineal. Sin embargo, requiere un gran número de muestras precisas para lograr los mejores resultados.
Interpolación de polinomios
La interpolación de polinomios puede utilizarse para lograr mediciones precisas sin necesidad de tomar muchas muestras. Este método utilizará muestras para encontrar una ecuación polinómica que proporcione una conversión precisa en todo el rango operativo del sensor.
The samples taken will be used to develop a polynomial equation that will describe the sensor output. At a minimum, you will need N-1 samples to derive a degree N polynomial. For example, 7 samples will create a degree 6 polynomial. You can also use more samples to create a lower degree polynomial, but this will generally have lower accuracy than creating a
higher degree polynomial with the same points.
Se puede utilizar cualquier número de muestras, pero recomendamos tomar al menos 3 muestras. Usar 2 muestras funcionaría, pero resultaría en una aproximación lineal. Tenga en cuenta que hay poca mejora en la precisión de los polinomios de grado 7 o superior.
While the polynomial can be determined manually, it is much easier to calculate it using software. One simple method is to use Microsoft Excel’s line of best fit; however, this will may not be precise enough for a usable conversion. Wolfram Alpha is a more accurate option, but the equation will still have to be solved manually. The best option is to use a programming library. For example, the Polynomial.fit() method from the NumPy Python library can be used. The code below shows how this can generate a 6th order polynomial from 7 points:
importar numpy.polynomial.polynomial coeficientes = numpy.polynomial.polynomial.polynomial.fit( 56668, 46553, 36140, 32845, 31207, 21913, 9586], # valores brutos 60, 42, 12, 0, -6, -36, -60], # valores de ángulo correspondientes a los valores brutos 6) # orden del polinomio impresión(coeficientes) # Salida: # [-7.88427627e+01 2.57631617e-03 -7.71958174e-08 -1.75354175e-13 # 2.17551410e-16 -5.89635260e-21 4.45379575e-26]
Tenga en cuenta que cuando se utiliza una función como esta, es importante especificar el orden correctamente. Por ejemplo, 4 muestras generarán un polinomio de 3er orden. Sin embargo, si se da 4 como el orden, la biblioteca hará una suposición aleatoria para crear una ecuación. Esto resultará en conversiones menos precisas.
The array returned by Polynomial.fit() are the coefficients of the polynomial. Based on the output above, the equation
would be:
Ángulo = (4.45e-26)x6- (5.89e-21)x5+ (2.17e-16)x4- (1.75e-13)x3- (7.72e-8)x2+ (2.57e-3)x1- 78.84
Esta función puede utilizarse para resolver ángulos desconocidos introduciendo el valor en bruto de x. Por ejemplo, digamos que tenemos la función anterior y tenemos una medida en bruto de 41643. Podemos encontrar el ángulo usando los siguientes cálculos:
Ángulo = (4.45e-26)(41643)6 - (5.89e-21)(41643)5 + (2.17e-16)(41643)4 - (1.75e-13)(41643)3 - (7.72e-8)(41643)2 + (2.57e-3)(41643)1 - 78.84
Ángulo = 232.264 - 738.402 + 654.227 - 12.663 - 133.868 + 107.285 - 78.842 = 30.002°.
If using the NumPy library shown above, this can be done using the polyval() method.
print(numpy.polynomial.polynomial.polyval(41643, coefficients.convert(.coef)) # Salida: 30.001695321007
Note that the result of this calculation is very sensitive to any change in input. For example, if the coefficients above are rounded to 3 significant digits (as written), the result of the equation is 31°. Because of this, it is important not to round any values while calculating the angle with this method.





