Description
Cette note d'application explique comment convertir en degrés la sortie brute d'un capteur d'inclinaison électrolytique.
Portée linéaire et plage de fonctionnement des capteurs d'inclinaison
An electrolytic tilt sensor’s measurement range can be described in two ways: linear range and operating range. The operating range is the range over which the sensor will give a monotonic output but otherwise has no defined characteristics (it is non-linear). The linear range is the portion of the operating range where the output is linear to within a certain percentage. Figure 1 shows the difference between the two ranges.
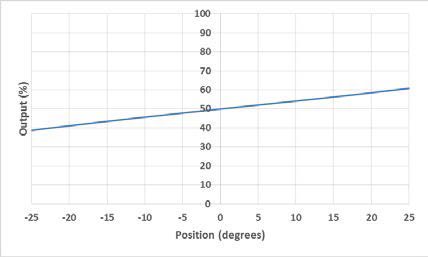
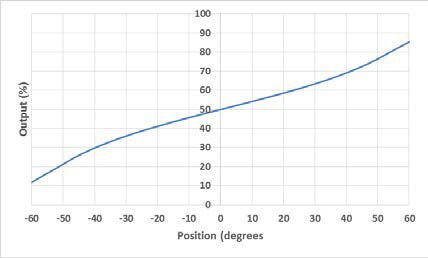
Figure 1 Portée linéaire (à gauche) et portée opérationnelle (à droite).
Approximation linéaire
To find the tilt angle within the linear range, it is necessary to find a linear function that matches the output of the sensor. This will be the function of the line in the left graph in Figure 1. This function is given below:
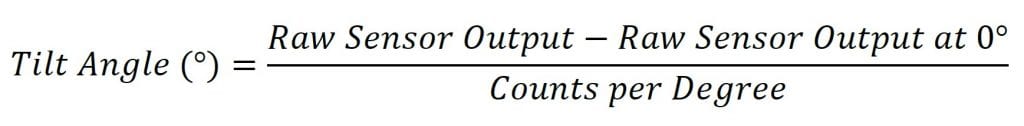
La sortie brute du capteur dans cette formule est la sortie du capteur. Elle est généralement exprimée en nombre, mais d'autres unités peuvent être utilisées en fonction de la façon dont la sortie du capteur est lue.
Les deux autres valeurs nécessiteront le prélèvement d'échantillons du capteur à certains angles. Ces angles peuvent être déterminés à l'aide d'un autre capteur, d'un rapporteur numérique ou de toute autre méthode de détermination des angles. La sortie brute du capteur à 0° n'est que la sortie lorsque le capteur est de niveau.
The counts per degree (which is the slope of the line) are calculated using the following formula:
![]()
The linear range is obtained from the datasheet for the sensor. The raw outputs will be the sensor output at the edges of the linear range. For example, for a sensor with a linear range of ±25°, the raw outputs would be sampled at +25° and -25°. Note that these samples will only need to be taken once to create the function; converting tilt can then be done using the sampled values.
Let’s say we have a 0717-4319-99 sensor with a 16-bit (0 to 65535) output we would like to convert to degrees. This is a dual axis sensor with a linear range of ±20°. Since it is a dual axis sensor, we will need 2 formulas: one for the X axis and one for the Y axis. First, we will find the X axis formula. We start be taking samples at 0° and ±20° and find the following measurements.
Inclinaison de l'axe X à -20° = 26055
Inclinaison de l'axe X à 0° = 33234
Inclinaison de l'axe X à ±20° = 40379
Nous pouvons maintenant utiliser ces échantillons pour calculer les comptes par degré :
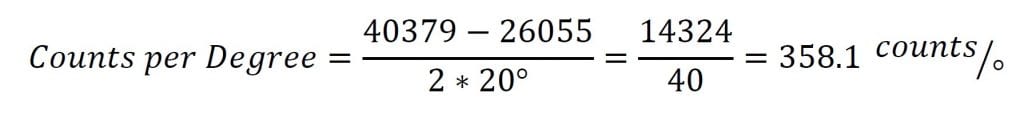
The counts per degree and zero samples can then be plugged into the formula to give the conversion below:

Si une mesure de l'axe des Y est nécessaire, suivez à nouveau ces étapes avec des échantillons de l'axe des Y.
Now, whenever we have a measurement from this sensor we would like to convert to degrees, we can use this new formula.
For example, if we have an X output of 29655, we can use the formula to determine the tilt angle:
![]()
Comptages approximatifs par diplôme
En raison de légères variations dues au processus de fabrication, la fonction de conversion doit être calculée pour chaque capteur spécifique. Cependant, cela n'est pas toujours possible. Le tableau ci-dessous indique les valeurs moyennes par degré et les valeurs 0° qui peuvent être utilisées dans les calculs. Notez que l'utilisation de ces valeurs donnera lieu à des mesures moins précises que la création d'une fonction pour le capteur spécifique. Toutes les valeurs sont pour une sortie de 16 bits (0-65535). Pour les capteurs qui ne figurent pas dans le tableau, l'utilisateur devra suivre la procédure ci-dessus pour trouver une conversion.
| Capteur | Comptage par degré | Zéro degré |
| ApexTwo™ | 284 | 32768 |
| F203-00A-212-00 | 17582 | 32768 |
| F225-00T-003-01 | 976 | 32768 |
| 0703-0711-99 | 17582 | 32768 |
| 0703-1602-99 | 976 | 32768 |
| 0703-1603-99 | 976 | 32768 |
| 0717-4303-99 | 736 | 32768 |
| 0717-4304-99 | 268 | 32768 |
| 0717-4305-99 | 188 | 32768 |
| 0717-4306-99 | 188 | 32768 |
| 0717-4311-99 | 268 | 32768 |
| 0717-4313-99 | 342 | 32768 |
| 0717-4314-99 | 335 | 32768 |
| 0717-4316-99 | 756 | 32768 |
| 0717-4317-99 | 569 | 32768 |
| 0717-4318-99 | 284 | 32768 |
| 0717-4319-99 | 363 | 32768 |
| 0717-4321-99 | 758 | 32768 |
| 0717-4322-99 | 594 | 32768 |
| 0729-1751-99 | 284 | 32768 |
| 0729-1752-99 | 284 | 32768 |
| 0729-1753-99 | 284 | 32768 |
| 0729-1754-99 | 284 | 32768 |
| 0729-1755-99 | 284 | 32768 |
| 0729-1759-99 | 284 | 32768 |
| 0729-1760-99 | 284 | 32768 |
| 0729-1765-99 | 976 | 32768 |
| 0729-1767-99 | 284 | 32768 |
| 0729-1768-99 | 284 | 32768 |
| 0729-1769-99 | 284 | 32768 |
| 0737-0101-99 | 2887 | 32768 |
| 0737-1203-99 | 41942-57670 | 32768 |
Interpolation multipoint
La méthode d'interpolation multipoint utilise des échantillons prélevés à l'avance pour obtenir la mesure en degrés. La précision de cette méthode dépendra du nombre et de la distribution des échantillons ; cependant, même le fait de prendre 3 échantillons donne généralement un meilleur résultat qu'une approximation linéaire.
Sample distribution is one of the most important factors in reaching an accurate conversion. Conversions close to samples will be more accurate. Because of this, samples taken closer together will result in more accurate conversions. These samples should be taken across the entire range of the sensor. Depending on the application, they can be evenly dispersed evenly across the entire range or focused in one region where precision is necessary.
To convert a raw value to degrees, identify two reference samples. These are the two samples that are closest to the measurement in each direction. Then, find a linear approximation between the two samples and map the raw output onto this approximation. The point on this line will give the sensor’s tilt in degrees. The graph in Figure 2 shows a visualization of this concept.
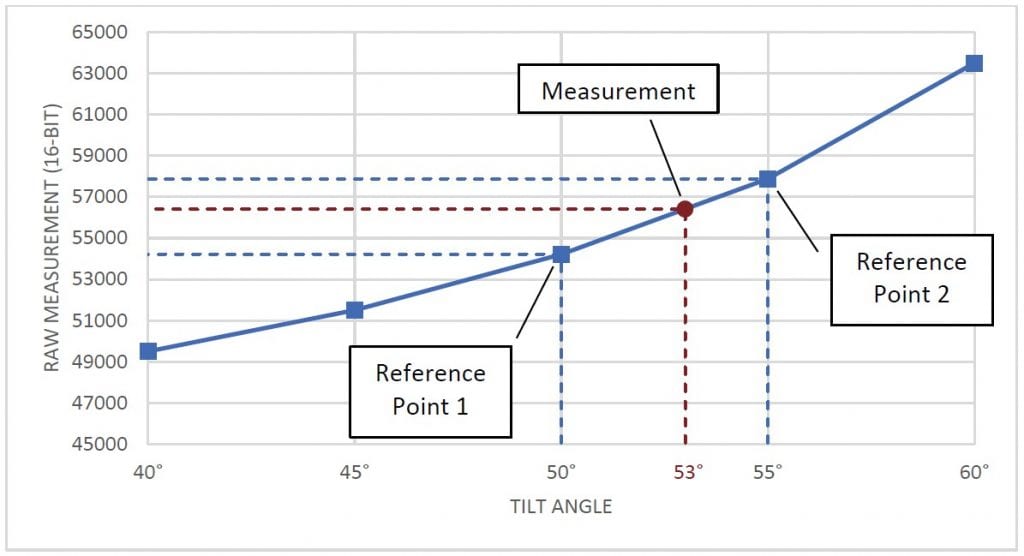
Figure 2 Graphique montrant les échantillons, les échantillons de référence et la mesure.
La formule de cette conversion est présentée ci-dessous.

Disons que nous avons une mesure brute de 56412 provenant d'un capteur d'inclinaison avec une plage de fonctionnement de ±60°. Supposons également que nous ayons déjà prélevé des échantillons à intervalles de 5° pour les utiliser pour la conversion. En comparant 56412 avec les échantillons, nous déterminons que nos deux points de référence seront à 50° (54213) et 55° (57878). Nous pouvons alors utiliser la formule pour calculer l'angle :
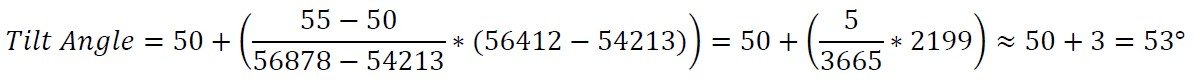
Par conséquent, notre mesure finale est de 53°.
Cette méthode peut être utilisée pour convertir en degrés les mesures prises n'importe où dans la plage de fonctionnement du capteur. Elle permet également d'obtenir une meilleure précision que l'approximation linéaire. Cependant, elle nécessite un grand nombre d'échantillons précis pour obtenir les meilleurs résultats.
Interpolation polynomiale
L'interpolation polynomiale peut être utilisée pour obtenir des mesures précises sans avoir à prélever de nombreux échantillons. Cette méthode utilisera des échantillons pour trouver une équation polynomiale qui fournira une conversion précise dans toute la gamme de fonctionnement du capteur.
The samples taken will be used to develop a polynomial equation that will describe the sensor output. At a minimum, you will need N-1 samples to derive a degree N polynomial. For example, 7 samples will create a degree 6 polynomial. You can also use more samples to create a lower degree polynomial, but this will generally have lower accuracy than creating a
higher degree polynomial with the same points.
Un nombre illimité d'échantillons peut être utilisé, mais nous recommandons de prélever au moins 3 échantillons. L'utilisation de 2 échantillons fonctionnerait, mais donnerait une approximation linéaire. Notez qu'il y a peu d'amélioration de la précision par rapport aux polynômes de degré 7 ou plus.
While the polynomial can be determined manually, it is much easier to calculate it using software. One simple method is to use Microsoft Excel’s line of best fit; however, this will may not be precise enough for a usable conversion. Wolfram Alpha is a more accurate option, but the equation will still have to be solved manually. The best option is to use a programming library. For example, the Polynomial.fit() method from the NumPy Python library can be used. The code below shows how this can generate a 6th order polynomial from 7 points:
import numpy.polynomial.polynomial coefficients = numpy.polynomial.polynomial.polynomial.fit( [56668, 46553, 36140, 32845, 31207, 21913, 9586], # valeurs brutes [60, 42, 12, 0, -6, -36, -60], # valeurs d'angle correspondant aux valeurs brutes 6) # ordre du polynôme imprimer(coefficients) # Sortie : # [-7.88427627e+01 2.57631617e-03 -7.71958174e-08 -1.75354175e-13 # 2.17551410e-16 -5.89635260e-21 4.45379575e-26]
Notez que lorsque vous utilisez une fonction de ce type, il est important de bien préciser l'ordre. Par exemple, 4 échantillons généreront un polynôme d'ordre 3. Cependant, si 4 est donné comme ordre, la bibliothèque fera une supposition aléatoire pour créer une équation. Cela se traduira par des conversions moins précises.
The array returned by Polynomial.fit() are the coefficients of the polynomial. Based on the output above, the equation
would be:
Angle = (4,45e-26)x6- (5,89e-21)x5+ (2,17e-16)x4- (1,75e-13)x3- (7,72e-8)x2+ (2,57e-3)x1- 78,84
Cette fonction peut ensuite être utilisée pour résoudre des angles inconnus en introduisant la valeur brute de x. Par exemple, disons que nous avons la fonction ci-dessus, et que nous avons une mesure brute de 41643. Nous pouvons trouver l'angle en utilisant les calculs suivants :
Angle = (4,45e-26)(41643)6 - (5,89e-21)(41643)5 + (2,17e-16)(41643)4 - (1,75e-13)(41643)3 - (7,72e-8)(41643)2 + (2,57e-3)(41643)1 - 78,84
Angle = 232,264 - 738,402 + 654,227 - 12,663 - 133,868 + 107,285 - 78,842 = 30,002
If using the NumPy library shown above, this can be done using the polyval() method.
print(numpy.polynomial.polynomial.polyval(41643, coefficients.convert(.coef)) # Sortie : 30.001695321007
Note that the result of this calculation is very sensitive to any change in input. For example, if the coefficients above are rounded to 3 significant digits (as written), the result of the equation is 31°. Because of this, it is important not to round any values while calculating the angle with this method.





