Descrizione
Questa nota applicativa spiega come convertire in gradi l'uscita grezza di un sensore di inclinazione elettrolitico.
Portata lineare e campo operativo dei sensori di inclinazione
An electrolytic tilt sensor’s measurement range can be described in two ways: linear range and operating range. The operating range is the range over which the sensor will give a monotonic output but otherwise has no defined characteristics (it is non-linear). The linear range is the portion of the operating range where the output is linear to within a certain percentage. Figure 1 shows the difference between the two ranges.
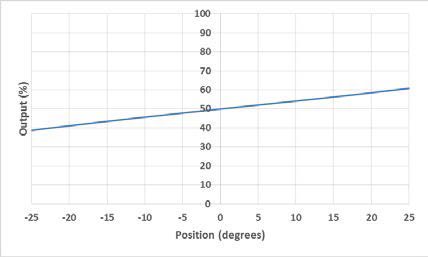
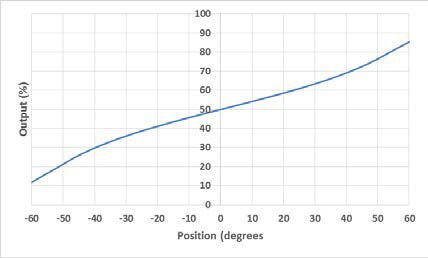
Figura 1 Gamma lineare (sinistra) e gamma operativa (destra).
Approssimazione lineare
To find the tilt angle within the linear range, it is necessary to find a linear function that matches the output of the sensor. This will be the function of the line in the left graph in Figure 1. This function is given below:
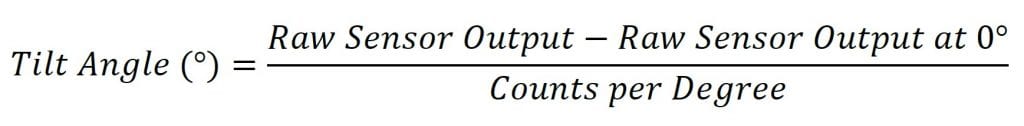
L'uscita del sensore grezzo in questa formula è l'uscita del sensore. Questa è di solito in conteggio, ma altre unità possono essere usate a seconda di come viene letta l'uscita del sensore.
Gli altri due valori richiedono il prelievo di campioni del sensore a determinate angolazioni. Questi angoli possono essere determinati utilizzando un altro sensore, un goniometro digitale o qualsiasi altro metodo per determinare gli angoli. L'uscita del sensore grezzo a 0° è solo l'uscita quando il sensore è in piano.
The counts per degree (which is the slope of the line) are calculated using the following formula:
![]()
The linear range is obtained from the datasheet for the sensor. The raw outputs will be the sensor output at the edges of the linear range. For example, for a sensor with a linear range of ±25°, the raw outputs would be sampled at +25° and -25°. Note that these samples will only need to be taken once to create the function; converting tilt can then be done using the sampled values.
Let’s say we have a 0717-4319-99 sensor with a 16-bit (0 to 65535) output we would like to convert to degrees. This is a dual axis sensor with a linear range of ±20°. Since it is a dual axis sensor, we will need 2 formulas: one for the X axis and one for the Y axis. First, we will find the X axis formula. We start be taking samples at 0° and ±20° and find the following measurements.
Inclinazione dell'asse X a -20° = 26055
X Inclinazione dell'asse a 0° = 33234
X Inclinazione dell'asse a ±20° = 40379
Ora possiamo usare questi campioni per calcolare i conteggi per grado:
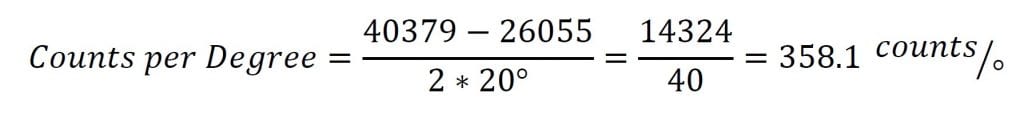
The counts per degree and zero samples can then be plugged into the formula to give the conversion below:

Se è necessaria una misurazione dell'asse Y, seguire di nuovo questi passi con i campioni dell'asse Y.
Now, whenever we have a measurement from this sensor we would like to convert to degrees, we can use this new formula.
For example, if we have an X output of 29655, we can use the formula to determine the tilt angle:
![]()
Conteggi approssimativi per grado
A causa di leggere variazioni causate dal processo di produzione, la funzione di conversione deve essere calcolata per ogni specifico sensore. Tuttavia, questo non è sempre possibile. La tabella seguente fornisce i conteggi medi per grado e i valori di 0° che possono essere utilizzati nei calcoli. Si noti che l'uso di questi valori comporterà misurazioni meno accurate rispetto alla creazione di una funzione per il sensore specifico. Tutti i valori sono per un'uscita a 16 bit (0-65535). I sensori non presenti nella tabella richiederanno all'utente di seguire la procedura sopra descritta per trovare una conversione.
| Sensore | Conteggi per grado | Zero gradi |
| ApexTwo™ | 284 | 32768 |
| F203-00A-212-00 | 17582 | 32768 |
| F225-00T-003-01 | 976 | 32768 |
| 0703-0711-99 | 17582 | 32768 |
| 0703-1602-99 | 976 | 32768 |
| 0703-1603-99 | 976 | 32768 |
| 0717-4303-99 | 736 | 32768 |
| 0717-4304-99 | 268 | 32768 |
| 0717-4305-99 | 188 | 32768 |
| 0717-4306-99 | 188 | 32768 |
| 0717-4311-99 | 268 | 32768 |
| 0717-4313-99 | 342 | 32768 |
| 0717-4314-99 | 335 | 32768 |
| 0717-4316-99 | 756 | 32768 |
| 0717-4317-99 | 569 | 32768 |
| 0717-4318-99 | 284 | 32768 |
| 0717-4319-99 | 363 | 32768 |
| 0717-4321-99 | 758 | 32768 |
| 0717-4322-99 | 594 | 32768 |
| 0729-1751-99 | 284 | 32768 |
| 0729-1752-99 | 284 | 32768 |
| 0729-1753-99 | 284 | 32768 |
| 0729-1754-99 | 284 | 32768 |
| 0729-1755-99 | 284 | 32768 |
| 0729-1759-99 | 284 | 32768 |
| 0729-1760-99 | 284 | 32768 |
| 0729-1765-99 | 976 | 32768 |
| 0729-1767-99 | 284 | 32768 |
| 0729-1768-99 | 284 | 32768 |
| 0729-1769-99 | 284 | 32768 |
| 0737-0101-99 | 2887 | 32768 |
| 0737-1203-99 | 41942-57670 | 32768 |
Interpolazione a più punti
Il metodo dell'interpolazione multipunto utilizza campioni prelevati in anticipo per ricavare la misura in gradi. La precisione di questo metodo dipenderà dal numero e dalla distribuzione dei campioni; tuttavia, anche prendendo 3 campioni si ottiene generalmente un risultato migliore di un'approssimazione lineare.
Sample distribution is one of the most important factors in reaching an accurate conversion. Conversions close to samples will be more accurate. Because of this, samples taken closer together will result in more accurate conversions. These samples should be taken across the entire range of the sensor. Depending on the application, they can be evenly dispersed evenly across the entire range or focused in one region where precision is necessary.
To convert a raw value to degrees, identify two reference samples. These are the two samples that are closest to the measurement in each direction. Then, find a linear approximation between the two samples and map the raw output onto this approximation. The point on this line will give the sensor’s tilt in degrees. The graph in Figure 2 shows a visualization of this concept.
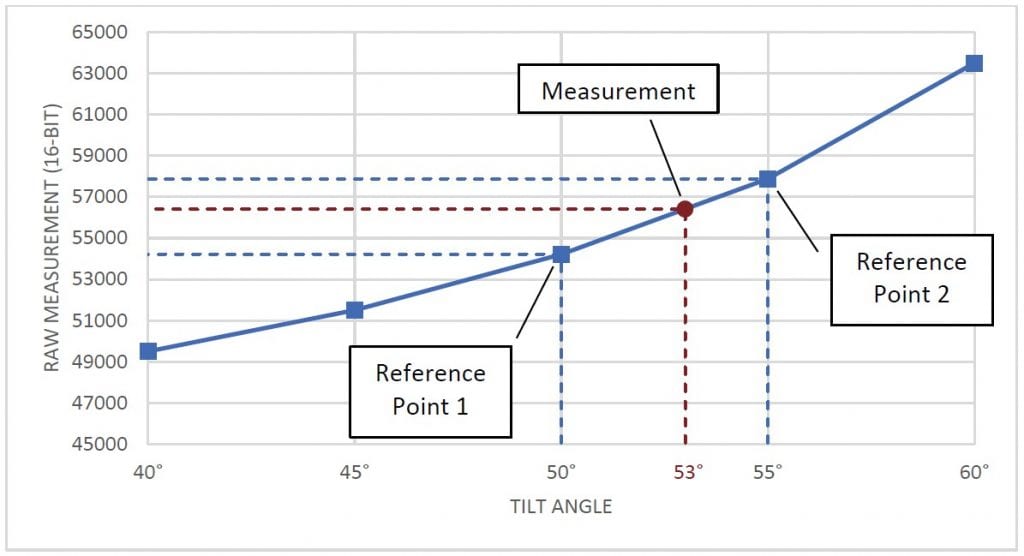
Figura 2 Grafico che mostra i campioni, i campioni di riferimento e la misurazione.
La formula di questa conversione è riportata di seguito.

Supponiamo di avere una misura grezza di 56412 da un sensore di inclinazione con un campo operativo di ±60°. Inoltre, supponiamo di aver già prelevato campioni a intervalli di 5° da utilizzare per la conversione. Confrontando 56412 con i campioni, determiniamo che i nostri due punti di riferimento saranno a 50° (54213) e 55° (5787878). Possiamo quindi utilizzare la formula per calcolare l'angolo:
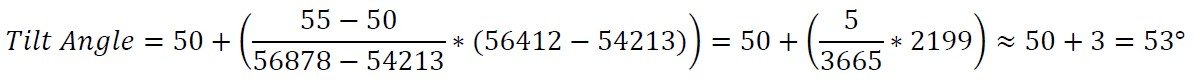
Pertanto, la nostra misurazione finale è di 53°.
Questo metodo può essere usato per convertire in gradi le misure da qualsiasi punto all'interno del campo operativo del sensore. Raggiungerà anche una migliore precisione rispetto all'approssimazione lineare. Tuttavia, richiede un gran numero di campioni accurati per ottenere i migliori risultati.
Interpolazione polinomiale
L'interpolazione polinomiale può essere utilizzata per ottenere misure accurate senza dover prelevare molti campioni. Questo metodo utilizzerà dei campioni per trovare un'equazione polinomiale che fornirà una conversione accurata attraverso il campo operativo del sensore.
The samples taken will be used to develop a polynomial equation that will describe the sensor output. At a minimum, you will need N-1 samples to derive a degree N polynomial. For example, 7 samples will create a degree 6 polynomial. You can also use more samples to create a lower degree polynomial, but this will generally have lower accuracy than creating a
higher degree polynomial with the same points.
È possibile utilizzare qualsiasi numero di campioni, ma si consiglia di prelevare almeno 3 campioni. L'utilizzo di 2 campioni funzionerebbe, ma darà luogo ad un'approssimazione lineare. Si noti che il miglioramento dell'accuratezza dei polinomi di grado 7 o superiore è minimo.
While the polynomial can be determined manually, it is much easier to calculate it using software. One simple method is to use Microsoft Excel’s line of best fit; however, this will may not be precise enough for a usable conversion. Wolfram Alpha is a more accurate option, but the equation will still have to be solved manually. The best option is to use a programming library. For example, the Polynomial.fit() method from the NumPy Python library can be used. The code below shows how this can generate a 6th order polynomial from 7 points:
importare polinomio.polinomio.intorpidito.polinomio.d'importazione coefficienti = numpy.polynomial.polynomial.fit( [56668, 46553, 36140, 32845, 31207, 21913, 9586], # valori grezzi [60, 42, 12, 0, -6, -36, -60], # valori angolari corrispondenti ai valori grezzi 6) # ordine di polinomio stampa(coefficienti) # Uscita: # [-7.88427627e+01 2.57631617e-03 -7.71958174e-08 -1.75354175e-13 # 2.17551410e-16 -5.89635260e-21 4.45379575e-26]
Si noti che quando si utilizza una funzione come questa, è importante specificare correttamente l'ordine. Ad esempio, 4 campioni genereranno un polinomio di 3° ordine. Tuttavia, se 4 è dato come ordine, la libreria farà un'ipotesi casuale per creare un'equazione. Questo risulterà in conversioni meno accurate.
The array returned by Polynomial.fit() are the coefficients of the polynomial. Based on the output above, the equation
would be:
Angolo = (4,45e-26)x6- (5,89e-21)x5+ (2,17e-16)x4- (1,75e-13)x3- (7,72e-8)x2+ (2,57e-3)x1- 78,84
Questa funzione può essere usata per risolvere angoli sconosciuti inserendo il valore grezzo di x. Per esempio, diciamo che abbiamo la funzione di cui sopra, e abbiamo una misura grezza di 41643. Possiamo trovare l'angolo usando i seguenti calcoli:
Angolo = (4,45e-26)(41643)6 - (5,89e-21)(41643)5 + (2,17e-16)(41643)4 - (1,75e-13)(41643)3 - (7,72e-8)(41643)2 + (2,57e-3)(41643)1 - 78,84
Angolo = 232.264 - 738.402 + 654.227 - 12.663 - 133.868 + 107.285 - 78.842 = 30.002°.
If using the NumPy library shown above, this can be done using the polyval() method.
print(numpy.polynomial.polyval(41643, coefficients.convert(.coef)) # Output: 30.001695321007
Note that the result of this calculation is very sensitive to any change in input. For example, if the coefficients above are rounded to 3 significant digits (as written), the result of the equation is 31°. Because of this, it is important not to round any values while calculating the angle with this method.





